How to Model a Problem (with Math!)
I have a weird problem that has a weird solution. The solution turns out to be more useful than I thought.
The Problem
I have a wide circle of friends, acquaintances, and colleagues, and I’m extroverted so I love talking to them all. But I’m also introverted, and I get super focused on whatever project I’m working on. Occasionally I’ll go incognito and when I pop up a month or two later people will ask “Hey man, what happened to you?” and I’ll say “Oh hey, I meant to get in touch, I just got focused on doing this or that or the other.”
I’ve had to create systems for myself to get tasks done, because when I focus, I seriously focus. I’ll forget to eat, forget to excerise, forget to call my mom. One thing I do is have a daily routine, like waking up at a certain time and going straight to the gym. If something happens everyday at the very beginning or very end of my day, I’ll do it.
The problem is that I’ll forget things that are supposed to happen in the middle of the day or things that don’t happen every day. Forget it if they are supposed to happen once a month.
For those things I use various alerts and alarms. I use my calendar extensively, and it e-mails me when something is about to happen. I use the alarm on my phone to remind me to do things throughout the day.
But that system sort of fails when it comes to managing my social life because that’s more complicated. How often should I get in touch with people? What should we do? It changes all the time and depends on the person. It’d be too much to try to track it all manually with a calendar, I don’t have time for that.
I want to be in regular contact with people, but I suck at it. I have a problem.
The Solution
So I thought, what if I had a tool that was like a Customer Relationship Management (CRM) app, but instead it was for personal relationships? More than just a contact list though, I want a tool to tell me when and how to contact everyone, individually on my list based on how close I am to that person.
This is weird because it takes an analytical approach to something people normally just wing. It feels strange to have a computer tell you when and how to reach out to your grandmother or potential girlfriend. But it just might work.
After I built the prototype, I realized the core technology wasn’t just a contact engine. It was actually an intermittent reinforcement engine. I could use it for staying in touch, for learning new things, for filtering my mailing list, and more.
I had something interesting.
I’m going to talk about the core tech here, but there’s a lot that needs to be added to this basic outline to make a useful product. Call me cynical, but I’m going to keep that secret sauce to myself. Still, I think the core idea is interesting and useful, and I want to share it.
Math follows. So much math.
Part 1: When?
The Idea
First I need to know when to get in touch with a given person. I want to talk to my best friend more than I want to talk to my cousin Larry, because I’m closer to my best friend. So I think frequency of contact should be based on an intimacy score.
I think it’s reasonable to say that intimacy can span from 0 to 100, 0 being not close at all, 100 being extremely intimate. So 100 would be, for example, your spouse, and you’d want multiple contacts per day. 0 would be a guy you used to know when you worked at Acme Corp several years ago who you want to maybe reach out to every year just to see if he’s got any interesting going on.
From those ranges I can conclude that the engine should return frequency in terms of hours, that range of the function is something like 12 (contact twice a day, every 12 hours) to 8,760 (contact once a year, there are 8,760 hours in a year).
The Numbers
From that range, I built the following table intuitively:
| Intimacy Score | Contact Frequency (Hours) | Explanation |
|---|---|---|
| 100 | 12 | twice a day |
| 90 | 168 | once a week |
| 75 | 336 | once every 2 weeks |
| 50 | 720 | once a month |
| 25 | 2,160 | once every 3 months |
| 10 | 5,760 | once every 8 months |
| 0 | 8,760 | once a year |
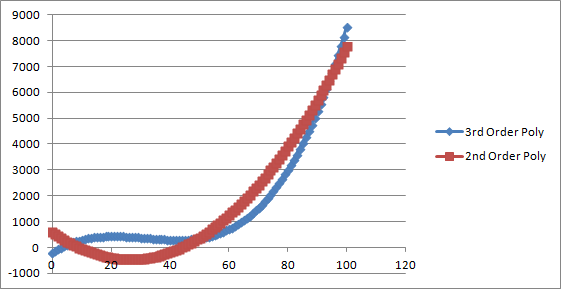
Those numbers just feel right to me. So I went about trying to find a function to fit the data. I reversed the intimacy
scores to make it easier so it’s actually 100-i, then I fit a couple polynomial curves to the data, both
3rd and 2nd order, but they gave strange results and actually went negative at one point in the
curve. The analysis gave these:
3rd Order Polynomial: 0.027674x3 - 2.63068x2 + 73.47367x - 167.7885523
2nd Order Polynomial: 1.520478x2 - 80.196x + 597.1004307
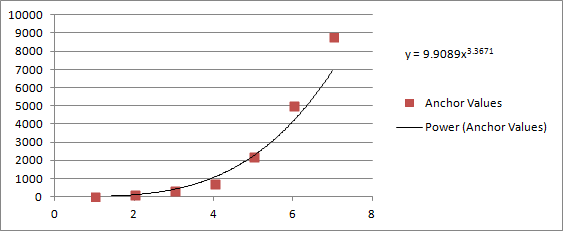
I also tried a power curve, but it fell too short of the goal amount:
Power: 9.9089x3.3671
Obviously I needed a curve that always went up with a positive second derivitive. What I was looking at was better fitted to an exponential curve, which yielded:
Exponential: 35.728e0.0564x
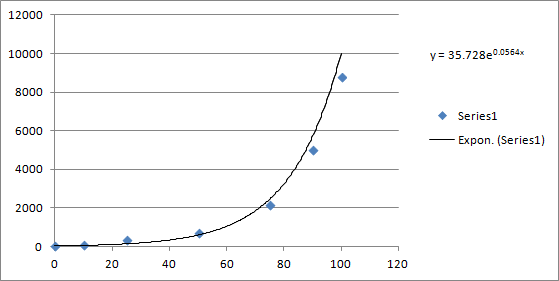
That gives us a range of 36 to 10,032 hours which is workable. To give some play, I added an adjustment term that lets us set the bottom end anywhere from 1 hour to the full 36 hours. Here’s the code:
def contact_frequency_in_hours intimacy, adjustment = 24
(35.728 * Math::E ** (0.0564 * (100 - intimacy))).round - adjustment
endThis function will tell you that you should get in touch with your wife every 12 hours, and your annoying cousin every 14 months or so.
Part 2: How?
The Idea
Now that we know how often to get in touch with someone, we have to know how we should get in touch. This problem is a little trickier.
The difference between ways of getting in touch with someone is fundamentally a difference in how effortful and impactful the contact is. You can text someone and you can also meet them for coffee. Depending on the person, you might want to only email them, or you might want to email them sometimes and other times get together with them. So we need to rotate through different types of contact according to how intimate you are, and we can categorize the contact types by impact. We’ll use the impact value as an index that maps to various contact methods that we’ll assign.
It’s arbitrary, but let’s say we have a range of 10 different impact levels, from 0 to 9, and say that they correspond to this:
| Impact | Contact Type |
|---|---|
| 0 | |
| 1 | Facebook Message |
| 2 | SMS Message |
| 3 | |
| 4 | Aim, GChat, etc. |
| 5 | Physical Letter |
| 6 | Phone |
| 7 | Skype Video Call |
| 8 | Group Face to Face |
| 9 | Face to Face |
So if you were to ask a person “How should you get in touch with your best friend this time?” he’d have to think about the last time he was in touch: “Well, I e-mailed him yesterday, maybe I should give him a call or go hang out with him.”
That means we’ll need to introduce another variable, which is the number of times you’ve contacted the person prior to this, because that will let us know how you should contact a person this time. Really what we need to know is how we contacted them last time, but since we have a deterministic function, we can fake it by just knowing the number of times we’ve been in contact.
The normal pattern of contact is to alternate between low and high impact methods (“I sent her a facebook message before, I’ll give her a call now”). That means we’ll need an occilating function like a sine wave.
The Numbers
I figured if I started to use this tool, I’d have a bunch of contacts to make all at once, so I started with a cosine, because I wanted to start with lower impact methods. In other words, with a sine wave, when x = 0, y = 1 (the maximum). That means when I haven’t been in touch before I should go for the highest impact contact method availble. That’s not what I want because then I’d have five billion face to face meetings all at once. With cosine, when x = 0, y = 0. Low impact.
The idea was right and sort of worked, but cosine is problematic for this application because its period is 2π which is a weird, irrational number. The values it’s going to be fed are always integers (the number of times we’ve been in contact), which means the cosine gave oscilating values, but they frequently skipped the bottom and top of the range because the x values don’t correpond reliably with the impact scores we expect.
So I went back to the drawing board and started using a triangle wave. It still oscillates but it does so consistently when you pass in integers.
The idea is that all the contact methods can be categorized from 1 to 10 according to their impact, and that the user should cycle through low and high impact contact methods (e.g. friends should sometimes e-mail, and other times get together for a beer). Using the triangle wave gives us the basic oscillation from high impact methods to low impact methods, given the number of times you’ve previously been in touch.
A basic triangle wave looks like this:
y = 2 / π * (cos-1(cos(π * number_of_previous_contacts)))
Which oscillates between y = 0 and y = 2 as number_of_previous_contacts increases.
The first thing to do is get the function in the correct range—we want it to have a total range of 10 instead of just 2, we have to multiply by 4.5 (so it goes from 0 to 9)
y = 4.5 * (2 / π) * (cos-1(cos(π * number_of_previous_contacts)))
We could shift the function from 0-9 to 1-10 but we’re probably going to return the actual contact method from a 0 indexed array, so we’ll leave it.
In theory this is good enough to return sane values, but there are a couple issues:
The range. If you are not intimate at all with someone, the algorithm recommends staying in touch about once per 14 or 15 months, but the way it works now is that it recommends you first tweet with them, then over the course of years send e-mails and SMS, until finally like 9 years after the first contact, you get together. That doesn’t make sense. So there needs to be a modifier that limits the amplitude, i.e. the range of possible contact methods. Look at the amplitude_modifier function below for details, but basically it makes contacts who have a less than 30 intimacy score rapidly switch from a 0-9 range to a 0-4 range.
y = amplitude_mod * (2 / π) * (cos-1(cos(π * number_of_previous_contacts)))
Finally, the aspect of the function that still doesn’t make sense is that we go back and forth between low and high impact methods, but as intimacy increases we want to have more high impact methods. So for example, the function as it is now would have intimate lovers start by tweeting and then escalate through emails and phone calls, until about 5 days later when they see each other again. What we really want is for them to get together more frequently, with some low impact contact in between. So that means literally increasing the frequency of our wave function, which you do by multiplying the number of previous contacts by something less than 1.
I’ve hard coded 0.5 in there as the frequency_modifier. Here’s why:
Reasonable modifiers would be in this form:
frequency_modifier / (amplitude_modifier * 2)
Where frequency_modifier could be any factor of the (amplitude_modifier * 2) in addition to the amplitude_modifier itself. If you graph this function out you’ll see what I mean, but the reason those values, and only those values, are good is that only those values return the highs and lows of the contact methods. If we used a different value, then it might not be possible to return, say, face to face meeting, because there is never an integer that would make this function return 9. That was the essential problem when this model used a cosine instead of a triangle wave.
So if we stick to the factors and the amplitude_modifier then we’ll always be able to get the right range, and even in between the highs and lows we tend to get integer y values, which is what we want. But lots of those “good” numbers still don’t make much sense. For example, if you have an amplitude modifier of 4.5 (i.e. the full range of 0-9), and the frequency_modifier is 1, then the hard coded .5 would be changed to 1/9th. If that were the case, then the function would return what I described above, slowly escalating contact between intimate lovers until, after maybe a week, they would meet face to face. That kind of interaction doesn’t make sense.
So just for demonstration, let’s go through all the possible values of the frequency modifier: 1 (we just talked about that), 3, 4.5, and 9 (all the factors of 9, plus the amplitude modifier of 4.5).
9 won’t work because 9/9 leads to this pattern: [lowest impact method, highest impact method, …]
That’s not like natural communication either.
3 is possibly ok, it gives this pattern: [1, 4, 7, 10, 7, 4, 1, …] so perhaps a SMS message, then e-mail, then phone call, then face to face meeting.
The other possibility is 4.5, which gives [1, 5, 10, 5, 1, …], so maybe an SMS message, IM chat, then face to face. Intuitively this made more sense than cycling through a litany of different contact types. Normally when you know a person, you have specific channels you generally use to contact them, so having 3 or 4 here makes sense.
The other issue is that when I compare all the other possible values:
| Amplitude Modifer | Frequency Modifiers |
|---|---|
| 2.5 | 1, 2.5, 5 |
| 3.0 | 1, 2, 3, 6 |
| 3.5 | 1, 3.5, 7 |
| 4.0 | 1, 2, 4, 8 |
| 4.5 | 1, 3, 4.5, 9 |
I don’t know how to calculate which factor to use if I want to use 3 for 4.5. Not all the amplitude modifiers have 4 factors. However, all the amplitude modifiers have themselves in the list, and those give me that pattern that seems right.
So it appears that I need to use the amplitude modifer as the frequency modifier in that term above, i.e.:
frequency_modifier / (amplitude_modifier * 2) ==
amplitude_modifier / (amplitude_modifier * 2)Which of course is always going to be 0.5. So I hard coded it:
y = amplitude_mod * (2 / π) * (cos-1(cos(π * number_of_previous_contacts * 0.5)))
Finally, here’s the code:
def contact_impact intimacy, number_of_previous_contacts
a_mod = amplitude_modifier intimacy
#f_mod = a_mod
a_mod * (2 / Math::PI) * (Math.acos(Math.cos(Math::PI * number_of_previous_contacts * 0.5)))
endAmplitude Modifer
The first thing to understand is that a full range of amplitude here is 10 units, i.e. 0-9, i.e. a modulus of 4.5. So the max we can return from this function is 4.5. So what we’re doing here is calculating how much of the full range we’re going to give based on the intimacy score.
The idea is to give most people the full range, but at some point along the intimacy scale, stop doing things like face to face get togethers, and stick to only email, or the like. In other words, if the intimacy is low, then the contact methods are going to be lower impact.
So, the function that gives us a basically straight line, then an increase, then straight line is the sigmoid function of the form:
y = 1 / (1 + e-intimacy)
But the range is wrong. The inflection point of the function is 0, which means you’d need a intimacy lower than 0 to have the full range. I want to move it over so that I can get sensible values if I enter a number from 0 to 100, instead of from -3 to 3. So I add a number to the exponent equal to the inflection point I want. I figure if someone is only 20% intimate, then that’s the cutoff, and the falloff should start around 30%, so that means the inflection point is 25%, which for this graph = 25:
y = 1 / (1 + e-intimacy + 25)
Now, this function outputs something from 0 to 1, but remember that the max we can output from this function is 4.5, and the minimum should be perhaps 2.5 (2.5 would mean the contact_impact function could return an impact rating from 0 to 4 since 2.5 * 2 is 5).
First of all, the range I want is from 4.5 to 2.5, which is 2 total, so I simply multiply by 2:
y = 1 / (1 + e-intimacy + 25) * 2
I don’t want really want 0 - 2 though, I want 2.5 - 4.5, so I just add my minimum of 2.5:
y = (1 / (1 + e-intimacy + 25) * 2) + 2.5
Now we have a function that outputs a value between 2.5 and 4.5, depending on the intimacy score.
The last bit is that the falloff is a little too “tight”, so we need to change e (which is about 2.7). The larger the value here, the tighter the falloff, which means that at some point on the intimacy scale you’d fall off a cliff and go from face to face contact, to only maybe e-mails. We want it to be a little more gradual, so instead of ~2.7 we’ll use 2 instead:
y = (1 / (1 + 2-intimacy + 25) * 2) + 2.5
The code:
def amplitude_modifier intimacy
inflection_point = 25
max_amplitude = 4.5
min_amplitude = 2.5
range_size = max_amplitude - min_amplitude
a_mod = ((1 / (1 + 2 ** (-intimacy + inflection_point))) * range_size) + min_amplitude
# The only sensible values for contact_impact to return are integers, so the amplitude needs to return something
# rounded to the nearest .5 (since the function multiplies the amplitude_modifier by 2)
(a_mod * 2).round / 2.to_f
endPutting it all together
Ok, so back to Earth. We want to know when and how to contact Aunt Betty. Here’s a method:
# returns the next time contact should take place, and what type of contact it should be
def next_contact intimacy, number_of_previous_contacts
impact = contact_impact(intimacy, number_of_previous_contacts)
return contact_frequency_in_hours(intimacy), get_contact_method_from_impact(impact)
endSo if we have an intimacy of 75 with Aunt Sue, and we’ve never been in touch:
next_contact(75,0) #=> 122, :facebook_messageIn a little over 5 days, we should send Aunt Sue a facebook message. That wasn’t so hard.
